Mathematische Zusammenhänge verstehen

Sekundarstufe I und II

Mathematik verstehen bedeutet nicht nur zu wissen, was man machen muss, sondern auch erklären zu können, warum man das so machen kann. Wer ein Konzept oder Verfahren verstanden hat, kann es versprachlichen und umgekehrt müssen Lernende Sprachmittel haben, um Konzepte oder Verfahren denken zu können. Sprache ist Ausdruck und Medium von Verstehen zugleich - sprachliches und fachliches Lernen im Mathematikunterricht sind somit untrennbar miteinander verbunden. Neben der kommunikativen Funktion von Sprache geht es hier also insbesondere um die kognitive Funktion von Sprache.
Warum das Verstehen so wichtig für nachhaltiges Lernen von Mathematik ist, wird im Bereich „Übergänge" erläutert.

* Bildquelle: Eisen, V., Kietzmann, U., Prediger, S., Sahin-Gür, D., Wilhelm, N. & Benholz, C. (2017). Sprachsensibles Unterrichten fördern im Fach Mathematik – Konzepte und Materialien für das Fachseminar. In S. Oleschko (Hrsg.), Sprachsensibles Unterrichten fördern: Angebote für den Vorbereitungsdienst (S. 190-227). Arnsberg: Landesweite Koordinierungsstelle Kommunale Integrationszentren.

Das kann man tun

Besonders sprachlich schwache Lernende - unabhängig von ihrer Herkunftsgeschichte - benötigen Unterstützung beim Sprachaufbau zum Lernen von Mathematik. Dabei kommt es darauf an, die knappe Zeit im Fachunterricht zielgerichtet zu nutzen, weshalb die Frage „welche Sprachmittel werden genau gebraucht" am Anfang des sprachsensiblen Unterrichts stehen sollte. Diese Frage muss für jedes Thema neu beantwortet werden (siehe dazu auch „Über Mathematik sprechen"). Dabei zeigt es sich, dass sogenannte bedeutungsbezogene Sprachmittel im Zentrum stehen sollten, also Worte und Satzbausteine, die eine Brücke zwischen Alltagssprache und Fachsprache bilden. Die Unterrichtsforschung hat übrigens klar gezeigt, dass gerade auch die starken Lernenden von einem in diesem Sinne sprachbildenden Mathematikunterricht profitieren!
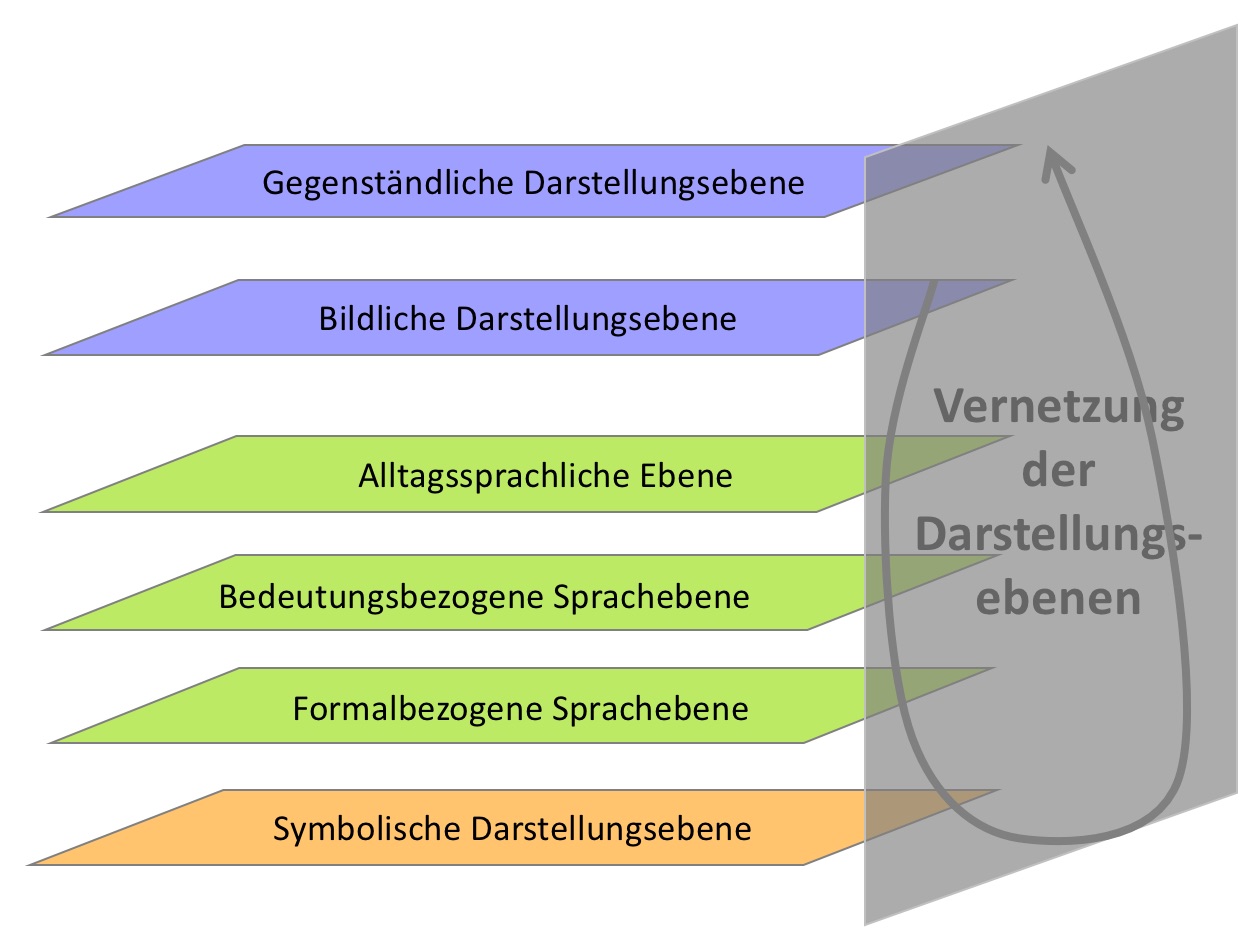
Bildquelle: DZLM

So können wir Sie unterstützen

  • Beratung und Begleitung von pädagogischem Fachpersonal
  • fachlicher Austausch in Netzwerktreffen
  • Workshops (online oder/und in Präsenz) zu folgenden Schwerpunkten (Kombinationen möglich):
    - Einführung in den sprachbildenden Mathematikunterricht
    - Darstellungsvernetzung zur integrierten Verstehens- und Sprachförderung
    - Einführung und Begleitung bei der Nutzung von ausgearbeiteten Unterrichtsreihen aus dem Pool des DZLM-Projekts Sprachbildung im Mathematikunterricht (SiMa)
  • Hospitationen sprachsensiblen (Mathematik-) Unterrichts in der Sek I
  • evaluierte Unterrichtssequenzen und Unterrichtsreihen
  • themenspezifische Blended-Learning-Angebote

Ein erster Zugang

Die beiden Arbeitsblätter zum Vergleichen von Brüchen bzw. zur bedingten Wahrscheinlichkeit geben exemplarische Einblicke, wie Darstellungsvernetzungsaufgaben den Verstehensaufbau unterstützen können (Auszüge aus Materialen des DZLM-Projekts Sprachbildung im Mathematikunterricht, SiMa).
Das Bild zu den Tauschaufgaben zeigt exemplarisch, wie Darstellungsvernetzung im Anfangsunterricht genutzt werden kann (Auszug aus einem Material des DZLM-Projekts PIKAS).

Externe Links

Der Einstiegsfilm "Warum & Wer" des Projekts Sprachbildung im Mathematikunterricht (SiMa) unseres Kooperationspartners DZLM erläutert die Bedeutung von Sprache für das Verstehen von Mathematik.

Weiterführendes

Beteiligte Netzwerke