Mathe verstehen
Potenziale entfalten durch Sprache(n)

Ankommen in der Sekundarstufe II

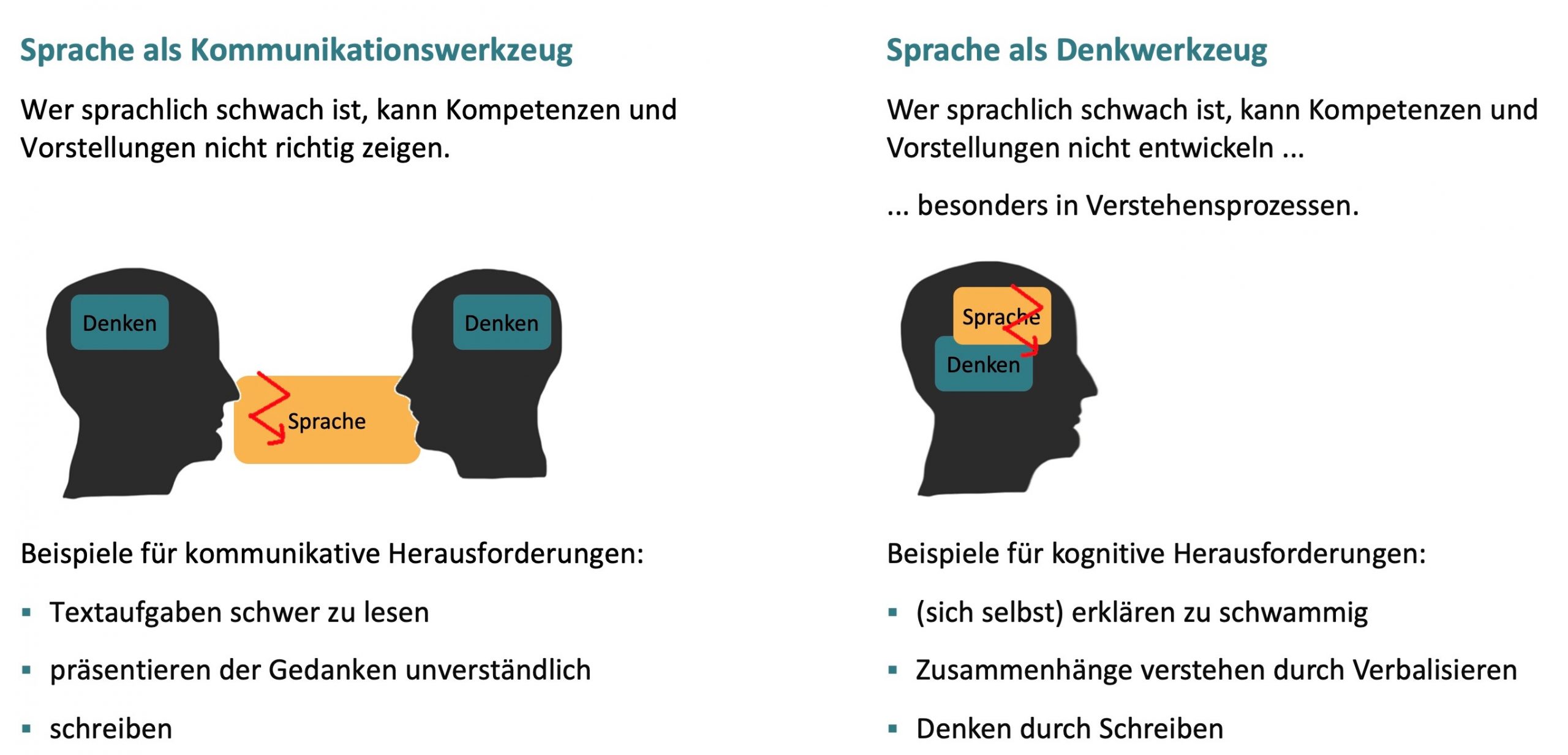
Um im Mathematikunterricht der Sekundarstufe II erfolgreich zu sein, ist ein solides Verständnis funktionaler Zusammen-hänge erforderlich. Aber auch andere Grundlagen, die in der Sekundarstufe I gelegt werden, sind für das Weiterlernen in der Sekundarstufe II relevant, zum Beispiel das Anteilsverständnis bei Brüchen für die Wahrscheinlichkeits-rechnung.

Zu Beginn der Einführungsphase werden häufig zentrale Inhalte der Sekundarstufe I zum Thema Funktionen aufgefrischt – ganz besonders an Gesamtschulen, die in der Sekundarstufe II oft viele Neuzugänge von anderen Schulen haben, oder an Weiterbildungskollegs, wo in der Sekundarstufe II viele Lernende mit extrem heterogenen Voraussetzungen neu einsteigen, deren Teilnahme am Unterricht der Sekundarstufe I teilweise schon mehrere Jahre zurückliegt.

Viele Lehrkräfte machen jedoch die Erfahrung, dass der Erfolg solcher Wiederholungen sehr begrenzt ist. Mögliche Ursachen hierfür sind:

  • Als Grundlage für den erfolgreichen Umgang mit Funktionen wird ein nachhaltiges Verständnis für funktionale Zusammenhänge (Funktionsbegriff) benötigt; die reine Kenntnis der Eigenschaften verschiedener Funktionen (die bei der Wiederholung oft im Fokus stehen) und die Bewältigung von Standardberechnungen mit verschiedenen Funktionstermen reicht hierfür nicht aus.
  • Bei einigen Lernenden können auch Lücken im Bereich des Verständnisses von Variablen und Größen vorhanden sein. Da der Funktionsbegriff darauf aufbaut, müsste das Aufholen zentraler SI-Grundlagen in dem Fall hier ansetzen.

Da in der Einführungsphase nur wenig Zeit zur Verfügung steht, um mögliche Verständnislücken aus der Sekundarstufe I zu beheben, ist eine genaue Standortbestimmung und gezielte Förderung der Verstehensgrundlagen für die benötigten Inhalte notwendig.

Im Mathematikunterricht der Sekundarstufe II gewinnt außerdem die konzeptionelle Vernetzung der verschiedenen Inhaltsbereiche an Bedeutung. Das spiegelt sich unter anderem in zunehmend komplexen Textaufgaben wider, für deren Bewältigung echtes Verstehen im Unterschied zur mechanischen Anwendung von Umformungs- und Rechenschritten unverzichtbar ist.

Das kann man tun

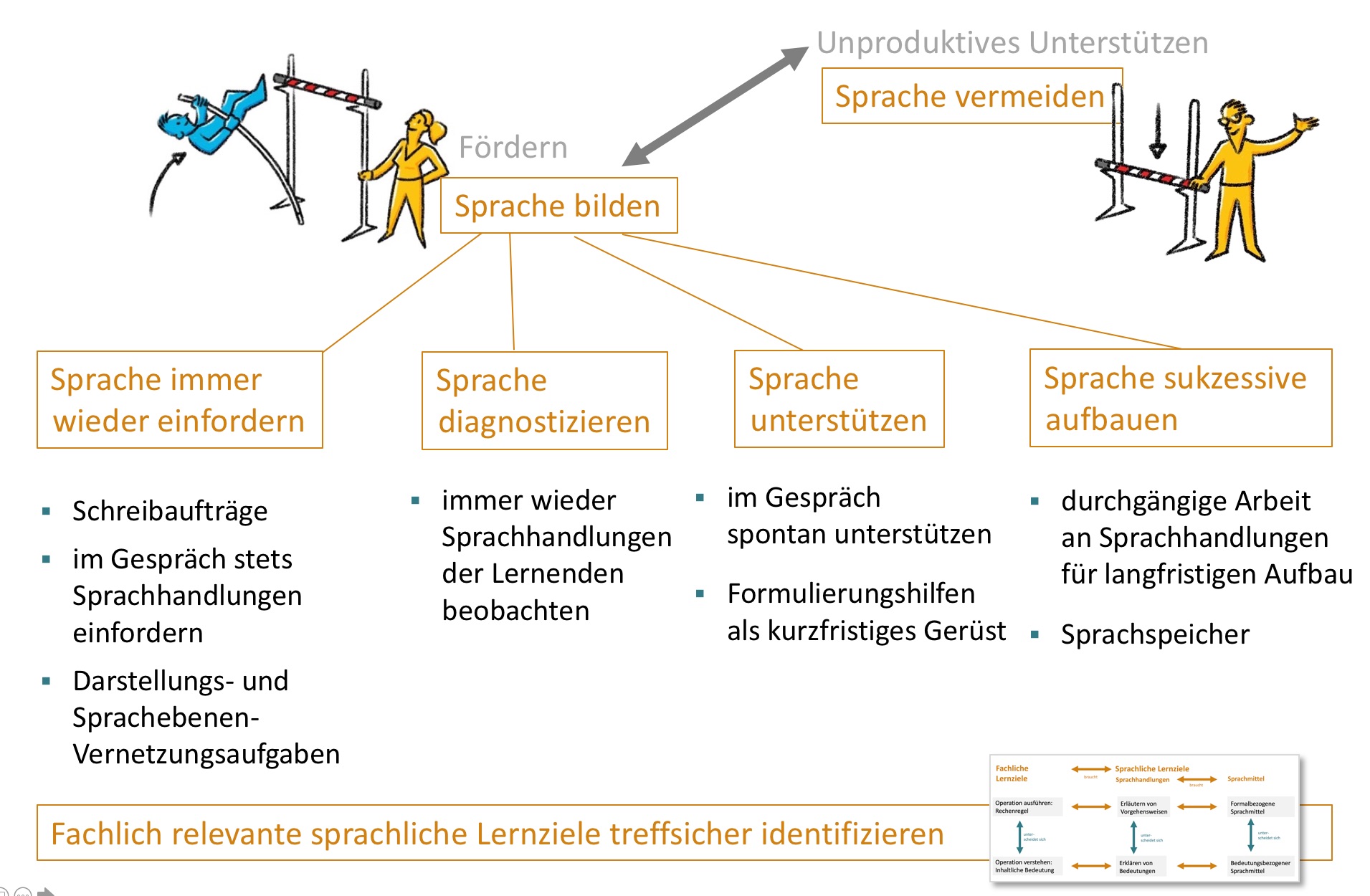
Variablen-, Term-, Gleichungs- und Funktionsverständnis lassen sich jeweils in verschiedene Teilaspekte unterteilen. Das Verständnis dieser Teilaspekte und anderer Grundlagen für den Unterricht in der Sekundarstufe II kann man separat diagnostizieren und gezielt aufbauen.

Für den Verständnisaufbau spielt die Sprache eine zentrale Rolle. In einem sprachbildenden Mathematikunterricht können Lehrkräfte Sprache und sprachsensible Ansätze gezielt einsetzen, um den Aufbau inhaltlichen Verständnisses zu unterstützen. Besonders sprachlich schwache Lernende – unabhängig von ihrer Herkunftsgeschichte – benötigen Unterstützung beim Sprachaufbau zum Lernen von Mathematik. Aber auch sprachlich Stärkere profitieren von sprachsensiblen Ansätzen im Mathematikunterricht, die auf den Aufbau von fachrelevanten Sprachmitteln ausgerichtet sind. Eine Verknüpfung von sprachlichen und fachlichen Lerninhalten im sprachbildenden Mathematikunterricht fördert nicht zuletzt auch das Verständnis und den sicheren Umgang mit Textaufgaben.

Verstehensfördernde sprachsensible Ansätze können somit im Mathematikunterricht genutzt werden, um

  • in der Einführungsphase der Sekundarstufe II fehlende Verständnisgrundlagen gezielt und zeitökonomisch aufzuarbeiten.
  • Lernende im Unterricht der Sekundarstufe I optimal auf den Unterricht in der Sekundarstufe II, aber auch auf die Anforderungen in der Zentralen Prüfung, vorzubereiten.

Um die Bewältigung von Textaufgaben zu unterstützen, kann man Lernende außerdem für die mathematische Bedeutung verschiedener sprachlicher Aspekte eines Aufgabentextes sensibilisieren sowie fachspezifische Lesestrategien im Mathematikunterricht vermitteln und einüben.

So können wir Sie unterstützen

  • Beratung und Begleitung von pädagogischem Fachpersonal
  • fachlicher Austausch in Netzwerktreffen (ggf. auch zu spezifischen Bedarfen des zweiten Bildungswegs)
  • Workshops (online oder/und in Präsenz) zu folgenden Schwerpunkten (Kombinationen möglich):
    • Einführung in den sprachbildenden Mathematikunterricht
    • diagnosegeleiteter Einstieg in die SII
    • Verständnis von Variablen, Termen und Gleichungen aufbauen
    • Funktionsverständnis aufbauen
    • Darstellungsvernetzung zur integrierten Verstehens- und Sprachförderung
    • Einführung und Begleitung bei der Nutzung von ausgearbeiteten Unterrichtsreihen aus dem Pool des DZLM-Projekts Sprachbildung im Mathematikunterricht (SiMa)
  • Hospitationen sprachsensiblen (Mathematik-) Unterrichts in der Sek I
  • evaluierte Unterrichtssequenzen und Unterrichtsreihen
  • themenspezifische Blended-Learning-Angebote

Ein erster Zugang

Das Arbeitsmaterial zu Linearen Funktionen (Auszug aus Materialen des DZLM-Projekts Sprachbildung im Mathematikunterricht, SiMa) ist für die Wiederholung von Grundlagen aus der SI in der Einführungsphase geeignet und zeigt, wie fachliches Verständnis durch gezielte Verknüpfung sprachlichen und fachlichen Lernens gefördert werden kann.

Die Diagnoseaufgaben zum Variablenverständnis aus dem Projekt Mathematik aufholen nach Corona unseres Kooperationspartners DZLM können genutzt werden, um z.B. zu Beginn der Einführungsphase zu ermitteln, ob einzelne Lernende eine Aufarbeitung von Verstehensgrundlagen in diesem Bereich benötigen.

WEITERFÜHRENDES

Beteiligte Netzwerke

1 1 Marker
7 1 Marker
7 2 Marker